前不久,百度发布了基于PaddlePaddle的深度强化学习框架PARL。git传送门
作为一个强化学习小白,本人怀着学习的心态,安装并运行了PARL里的quick-start。不体验不知道,一体验吓一跳,不愧是 NeurIPS 2018 冠军团队的杰作,代码可读性良好,函数功能非常清晰,模块之间耦合度低、内聚性强。不仅仅适合零基础的小白快速搭建DRL环境,也十分适合科研人员复现论文结果。
废话不多说,我们从强化学习最经典的例子——迷宫寻宝(俗称格子世界GridWorld)开始,用策略梯度(Policy-Gradient)算法体验一把PARL。
模拟环境
强化学习适合解决智能决策问题。如图,给定如下迷宫,黑色方格代表墙,黄色代表宝藏,红色代表机器人;一开始,机器人处于任意一个位置,由于走一步要耗电,撞墙后需要修理,所以我们需要训练一个模型,来告诉机器人如何避免撞墙、并给出寻宝的最优路径。
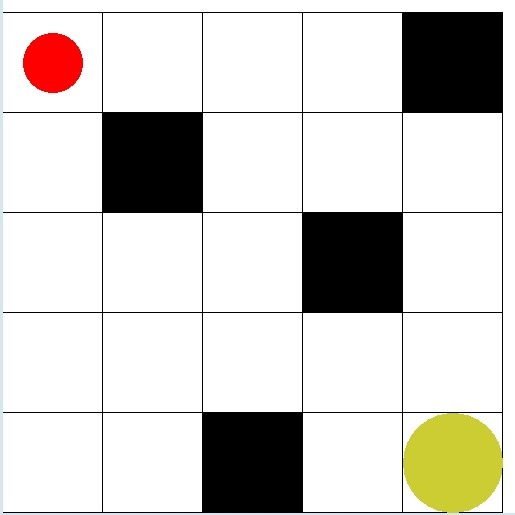
接下来,定义强化学习环境所需的各种要素:状态state、动作action、奖励reward等等。
state就是机器人所处的位置,用(行、列)这个元组来表示,同时可以表示墙:
self.wallList=[(2,0),(3,2),(1,3),(4,4)]
self.start=(0,4)
self.end=(4,0)
使用random-start策略实现reset功能,以增加初始状态的随机性:
def reset(self):
for _ in range(0,1024):
i=np.random.randint(self.row)
j=np.random.randint(self.col)
if (i,j) not in self.wallList and (i,j)!=self.end:
self.pos=(i,j)
break
return self.pos
定义动作action,很显然,机器人可以走上下左右四个方向:
action_dim=4
dRow=[0,0,-1,1]
dCol=[1,-1,0,0]
定义奖励reward,到达终点奖励为10,走其他格子需要耗电,奖励为-1:
def reward(self, s):
if s == self.end:
return 10.0
else:
return -1.0
另外,越界、撞墙需要给较大惩罚:
if not checkBounds(nextRow, nextCol) :
#越界
return self.pos, -5.0, False, {'code':-1,'MSG':'OutOfBounds!'}
nextPos=(nextRow,nextCol)
if meetWall(self.wallList, nextPos):
#撞墙
return self.pos, -10.0, False, {'code':-1,'MSG':'MeetWall!'}
至此,强化学习所需的状态、动作、奖励均定义完毕。接下来简单推导一下策略梯度算法的原理。
策略梯度(Policy-Gradient)算法是什么?
我们知道,强化学习的目标是给定一个马尔可夫决策过程,寻找出最优策略。所谓策略是指状态到动作的映射,常用符号 $\pi$表示,它是指给定状态 s 时,动作集上的一个分布,即: $$\pi (a|s)=p[A{t}=a|S{t}=s]$$
策略梯度的做法十分直截了当,它直接对求解最优策略进行参数化建模,策略p(a|s)将从一个概率集合变成一个概率密度函数p(a|s,θ),即:$$\pi_{\theta}=p[a|s,\theta]$$
这个策略函数表示,在给定状态s和参数θ的情况下,采取任何可能动作的概率,它是一个概率密度函数,在实际运用该策略的时候,是按照这个概率分布进行动作action的采样的,这个分布可以是离散(如伯努利分布),也可以说是连续(如高斯分布)。最直观的方法,我们可以使用一个线性模型表示这个策略函数: $$\pi _{\theta }=\phi (s)*\theta$$
其中,$\phi(s)$表示对状态s的特征工程,θ是需要训练的参数。这样建模有什么好处呢?其实最大的好处就是能时时刻刻学到一些随机策略,增强探索性exploration。
为什么可以增加探索性呢?
比如迷宫寻宝问题,假设一开始机器人在最左上角的位置,此时p(a|s,θ)可以初始化为[0.25,0.25,0.25,0.25],表明机器人走上、下、左、右、的概率都是0.25。当模型训练到一定程度的时候,p(a|s,θ)变成了[0.1,0.6,0.1,0.2],此时,向下的概率最大,为0.6,机器人最有可能向下走,这一步表现为利用exploitation;但是,向右走其实也是最优策略,0.2也是可能被选择的,这一步表现为探索exploration;相对0.6和0.2,向上、向左两个动作的概率就小很多,但也是有可能被选择的。如果模型继续训练下去,p(a|s,θ)很有可能收敛成[0.05,0.45,0.05,0.45],此时,机器人基本上只走向下或者向右,选择向上、向左的可能性就极小了。这是最左上角位置(状态)的情况,其他状态,随着模型的训练,也会收敛到最优解。
有了模型,就想到求梯度,那么,如何构建损失函数呢?标签y-Target又是什么?
一个非常朴素的想法就是:如果一个动作获得的reward多,那么就使其出现的概率变大,否则减小,于是,可以构建一个有关状态-动作的函数 f(s,a) 作为损失函数的权重,这个权重函数可以是长期回报G(t),可以是状态值函数V(s),也可以是状态-行为函数Q(s,a),当然也可以是优势函数A。但是,这个权重函数和参数θ无关,对θ的梯度为0,仅仅作为p(a|s,θ)的系数。
现在考虑模型的输出$\pi(a|s,θ)$,它表示动作的概率分布,我们知道,智能体每执行完一轮episode,就会形成一个完整的轨迹Trajectory: $$T=[S{0},a{0},P(S{1}|S{0},a{0}),S{1},a{1},P(S{2}|S{1},a{1}),S{2}...S{n-1},a{n-1},P(S{n}|S{n-1},a{n-1}),S{n}]$$ 其中,状态$S{0},S_{1}...S{n}$和参数θ无关,状态转移概率P(s'|s,a)是由环境所决定的,和参数θ也无关。所以,我们的目标简化为:优化参数θ,使得每个动作概率的乘积$p(a{0})p(a{1})...p(a{n})$达到最大,即使得$\pi (a{0}|s{0},\theta)\pi (a{1}|s{1},\theta)\pi (a{2}|s{2},\theta)...*\pi (a{n}|s{n},\theta)$这个累乘概率达到最大,可用如下公式表示:$$Maximize[arg(\theta )],T=\prod{t=0}^{N}\pi (a|s{t},\theta)$$
这显然是我们熟悉的极大似然估计问题,转化为对数似然函数: $$log(T)=log(\prod{t=0}^{N}\pi (a|s{t},\theta))=\sum{t=0}^{N}log(\pi (a|s{t},\theta))$$
乘以权重 f(s,a),构建如下目标函数,这个目标函数和我们平时见到的损失函数正好相反,它需要使用梯度上升的方法求一个极大值: $$J(\theta )=\sum{t=0}^{N}log(\pi(a |s{t},\theta) )*f(s,aTrue)$$
注意到,这里的aTrue就是标签y-Target,表示agent在状态$s_{t}$时真实采取的动作,可以根据轨迹trajectory采样得到。
学过机器学习的同学都知道,一般用目标函数的均值代替求和,作为新的目标函数: $$J(\theta )=\frac{1}{N}\sum{t=0}^{N}log(\pi (a|s{t},\theta ))*f(s_{t},aTrue)$$
均值,就是数学期望,所以目标函数也可以表示为: $$J(\theta )=E{\pi (\theta )}(log(\pi (a|s{t},\theta ))*f(s_{t},aTrue))$$
有了目标函数,梯度就很容易计算了,由于$f(s{t},a)$对于θ来说是系数,故梯度公式如下: $$\triangledown J(\theta )=E{\pi(\theta)}(\triangledown log(\pi(a|s{t},\theta))*f(s{t},aTrue))$$
那么,策略$\pi$具体的表现形式如何?前文提到,策略可以是离散的,也可以是连续的,不妨考虑离散的策略。由于我们需要求解最大值问题,也就是梯度上升问题,自然而然就想到把梯度上升问题转化为梯度下降问题,这样才能使得目标函数的相反数达到最小,而什么样的函数可以将梯度下降和对数函数关联起来呢?显然是我们熟悉的交叉熵,所以最终的损失函数确定为: $$Minimize[arg(\theta)],J(\theta)=E_{\pi(\theta)}(CrossEntropy(\pi(a|s{t},\theta),aTrue)*f(s{t},aTrue))$$
连续策略的推导与离散策略类似,有兴趣的读者可以参考相关文献。
自此,公式推导可以告一段落。策略梯度的基本算法就是Reinforce,也称为蒙特卡洛策略梯度,简称MCPG,PARL的官方policy-gradient就是基于以下算法框架实现的:

PARL源码结构
在搭建模型之前,我们先分析一下PARL的主要模块:
1. env:环境,在这里,我们的环境就是迷宫寻宝
2. model:模型,可以是简单的线性模型,也可以是CNN、RNN等深度学习模型
3. algorithm:算法,对model层进行封装,并利用模型进行predict(预测),同时构建损失函数进行learn(学习);具体实现形式可以是DQN、PG、DDPG等等
4. agent:智能体,对algorithm层进行封装,一般也包含predict、learn两个函数;同时,由于智能体要同时进行探索exploration-利用exploitation,还经常包含一个sample函数,用于决定到底是randomSelect(随机选择或者根据分布函数选择动作),还是argmax(100%贪心,总是选择可能性最大的动作)
5. train:训练和测试,用于实现agent和环境的交互,当模型收敛后,可以测试智能体的准确性
6. utils:其他辅助功能
以下的架构示意图,可以帮助我们更好的理解PARL:
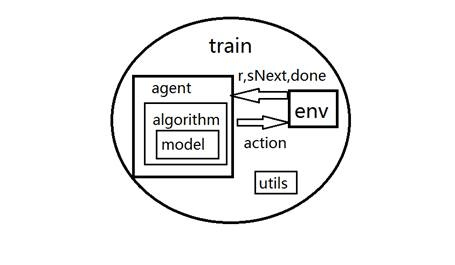
代码实现&源码解读
在理解了框架的各个模块之后,我们就可以按照模板填代码了,学过MVC、ORM等框架的同学都知道,这是一件非常轻松愉快的事情。
1、MazeEnv。迷宫环境,继承自gym.Env,实现了reset、step、reward、render四个主要方法,这里不再赘述
2、MazeModel。模型层,搭建如下全链接神经网络,输入是状态state-input,输出是策略函数action-out,由于策略函数是动作的概率分布,所以选用softmax作为激活函数,中间还有若干隐藏层。
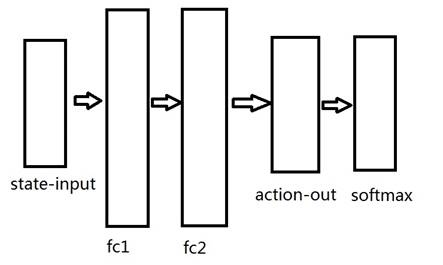
代码实现非常的简单,让MazeModel继承官方的Model类,然后照猫画虎搭建模型即可:
class MazeModel(Model):
def __init__(self, act_dim):
self.act_dim = act_dim
hid1_size = 32
hid2_size = 32
self.fc1 = layers.fc(size=hid1_size, act='tanh')
self.fc2 = layers.fc(size=hid2_size, act='tanh')
self.fcOut = layers.fc(size=act_dim,act='softmax')
def policy(self, obs):
out = self.fc1(obs)
out = self.fc2(out)
out = self.fcOut(out)
return out
3、policy_gradient。算法层;官方仓库提供了大量的经典强化学习算法,我们无需自己重复写,可以直接复用算法库(parl.algorithms)里边的PolicyGradient 算法!
简单分析一下policy_gradient的源码实现。
define_predict函数,接收状态obs,调用model的policy方法,输出状态所对应的动作:
def define_predict(self, obs):
""" use policy model self.model to predict the action probability
"""
return self.model.policy(obs)
define_learn函数,接收状态obs、真实动作action、长期回报reward,首先调用model的pocliy方法,预测状态obs所对应的动作概率分布act_prob,然后使用交叉熵和reward的乘积构造损失函数cost,最后执行梯度下降法,优化器为Adam,完成学习功能:
def define_learn(self, obs, action, reward):
""" update policy model self.model with policy gradient algorithm
"""
act_prob = self.model.policy(obs)
log_prob = layers.cross_entropy(act_prob, action)
cost = log_prob * reward
cost = layers.reduce_mean(cost)
optimizer = fluid.optimizer.Adam(self.lr)
optimizer.minimize(cost)
return cost
4、MazeAgent。智能体。其中,self.pred_program是对algorithm中define_predict的简单封装,self.train_program是对algorithm中define_learn的简单封装,我们可以参考官方的CartpoleAgent实现,按照框架模板填入相应的格式代码。
这里,仅仅分析self.pred_program,self.train_program写法类似:
self.pred_program = fluid.Program()#固定写法
with fluid.program_guard(self.pred_program):
obs = layers.data(
name='obs', shape=[self.obs_dim], dtype='float32')#接收外界传入的状态obs
self.act_prob = self.alg.define_predict(obs)
#调用algorithm的define_predict,self.act_prob为动作的概率分布
sample函数,注意这句话:
act = np.random.choice(range(self.act_dim), p=act_prob)
这句话表示根据概率分布随机选出相应的动作;假设上、下、左、右的概率分别为[0.5,0.3,0.15,0.05],那么上被选择的概率是最大的,右被选择的概率是最小的,所以sample函数既能exploration,又能exploitation,体现了强化学习中的探索-利用的平衡。
predict函数,和sample函数不同的是,它总是贪心的选择可能性最大的动作,常常用于测试阶段:
act = np.argmax(act_prob)
learn函数,接收obs、action、reward,进行批量梯度下降,返回损失函数cost
5、TrainMaze。让环境env和智能体agent进行交互,最主要的部分就是以下代码,体现了MCPG过程:
#迭代十万个episode
for i in range(1,100001):
#采样
obs_list, action_list, reward_list = run_train_episode(env, agent)
#使用滑动平均的方式计算奖励的期望
MeanReward=MeanReward+(sum(reward_list)-MeanReward)/i
batch_obs = np.array(obs_list)
batch_action = np.array(action_list)
#通过backup的方式计算G(t),并进行归一化处理
batch_reward = calc_discount_norm_reward(reward_list, GAMMA)
#学习
agent.learn(batch_obs, batch_action, batch_reward)
其中,滑动平均可以选择任意一个公式,无偏估计表示真实的均值,有偏估计更加接近收敛后的平均奖励:
无偏估计: $E{X}=E{X}+(x-E_{X})/N$
有偏估计: $E{X}=(1-\alpha )E{X}+(x-E_{X})*\alpha$,α是学习率,取0.1、0.01等等
其他代码都是辅助功能,如记录log、画图、渲染环境等等。
运行程序并观察结果
运行TrainMaze,可以看到如下输出。
1、训练之前,机器人并不知道如何寻宝,所以越界、撞墙次数非常多,也绕了很多弯路,平均奖励比较低
ErrorCountBeforeTrain:25052 #越界+撞墙次数
平均奖励曲线:
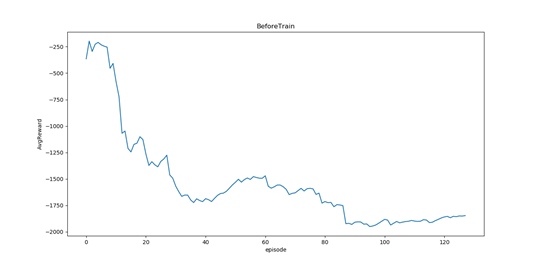
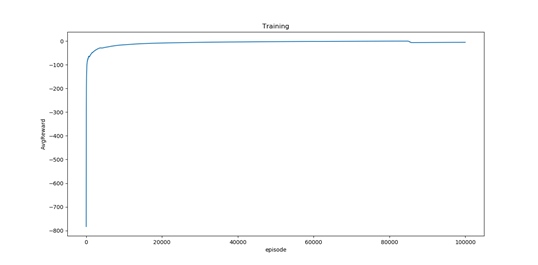
2、训练模型。迭代十万个episode,观察如下学习曲线,纵轴表示平均奖励,可以看到,模型已经收敛了:
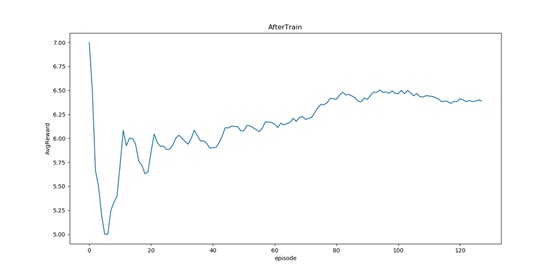
3、测试模型的准确性。测试阶段,我们迭代128轮,智能体几乎没有任何越界或者撞墙行为,由于是random-start,所以平均奖励有少许波动,但稳定在5-7之间。
ErrorCountAfterTrain:0 #没有任何撞墙或者越界
训练后的平均奖励:
如下动画展示了训练成果,可以看到,无论从哪个位置开始,机器人都能轻松绕过障碍物,并以较快的速度找到宝藏,我们的agent终于有了智能决策能力!

源码Git地址
https://github.com/kosoraYintai/PARL-Sample
参考文献:
· CS 294-112 at UC Berkeley,Deep Reinforcement Learning.
· Deepmind,Silver.D,Reinforcement Learning Open Class.
· 冯超. 强化学习精要[M]. 北京:电子工业出版社,2018.
· 郭宪,方勇纯. 深入浅出强化学习[M]. 北京:电子工业出版社,2018.



